お風呂の保温機能について 再考
毎度のお付き合いをありがとうございます。![]()
さて、お風呂の話題が続いておりますが、これまでの計算が感覚論でデータを考えてたので、
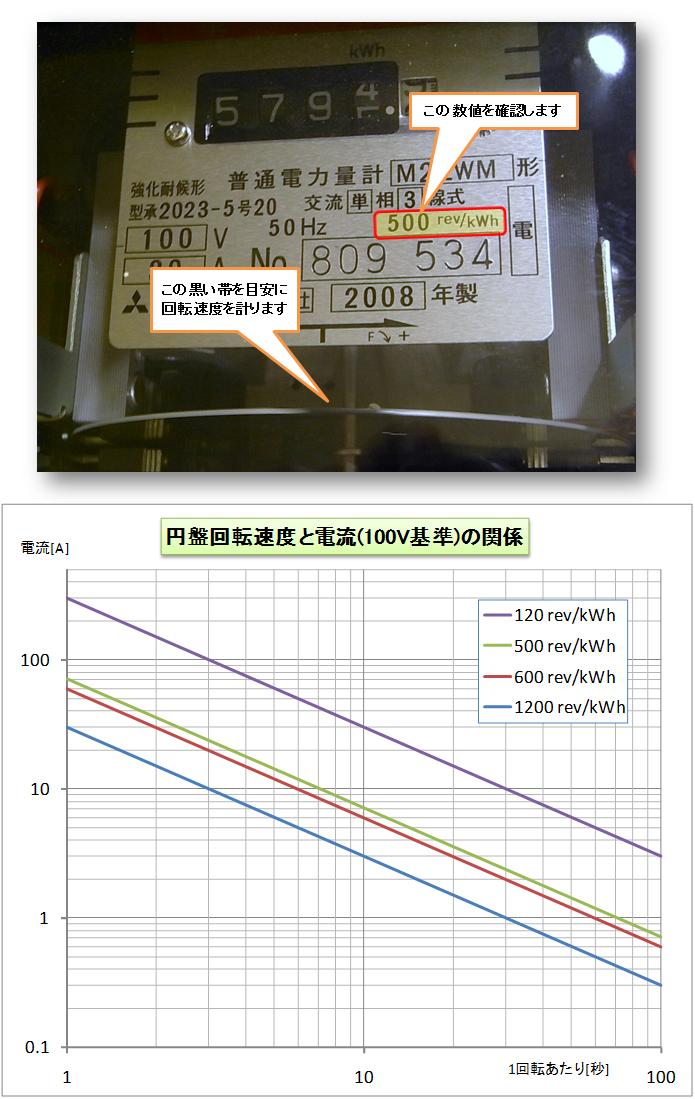
技術屋としては、やはり実測データが必要と感じ、昨日我が家のお風呂で実験を試みました。![]()
驚いたことに、
お風呂の落としブタの効果も手伝ってか、お湯がなかなか冷めないのです。
どうやら我が家の浴槽は、断熱タイプ(★)のものらしく、1時間で1℃程度の
冷め方でした。(★浴槽の裏側にウレタン樹脂を吹き付けたもの)![]()
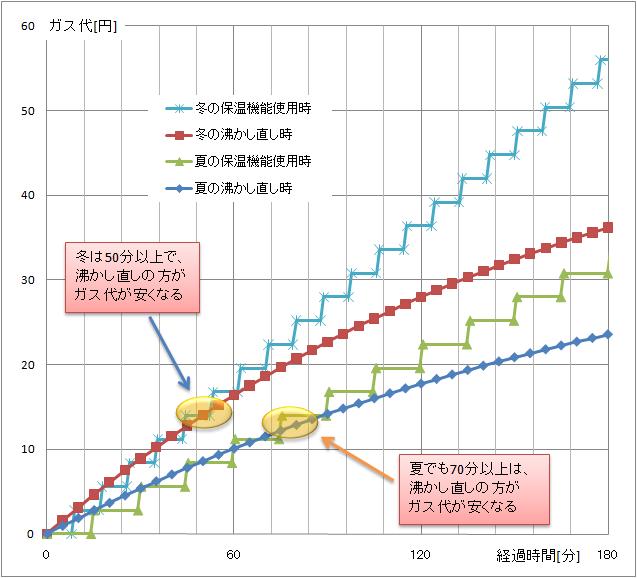
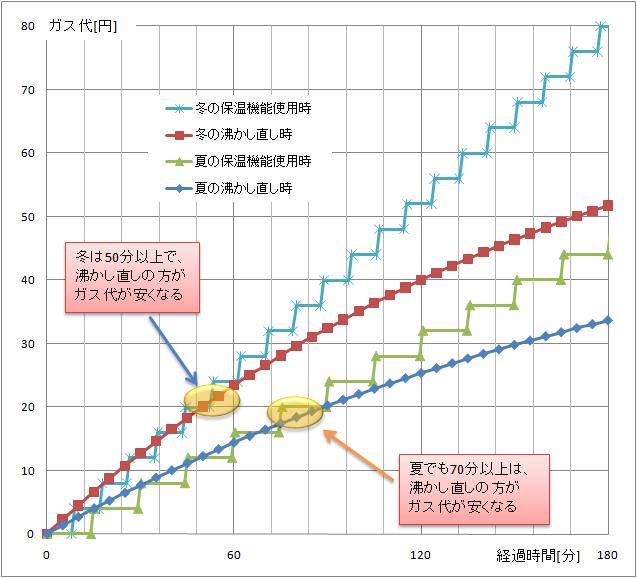
この辺りを考慮して、再度グラフ化したのが下です。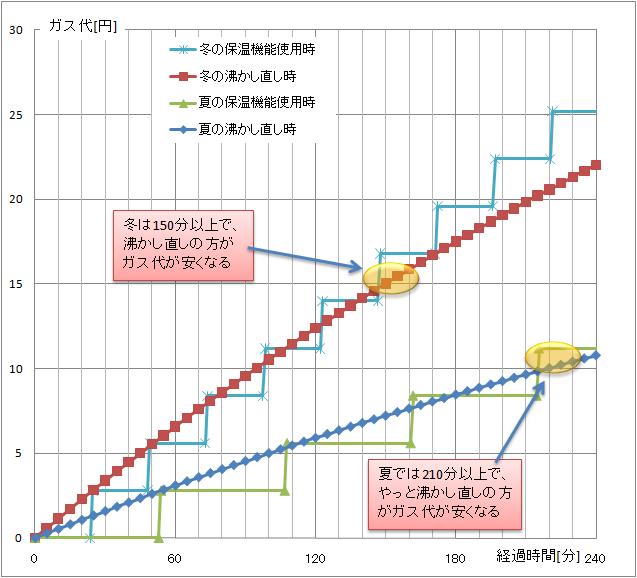
これによると、夏場は3時間以上保温にしても、沸かし直しと大差なく、
冬場でも、2時間半は保温の方がコストが優位となりました。
結論として、お風呂の浴槽や、お風呂自体の環境(熱の伝わり方)によって、
使い方が大きく左右されるようです。
いわゆる、シテスムバスタイプは、ほとんどが我が家と同様のものだと
思われますので、保温機能も便利に使って良いようです。
昔ながらのコンクリートやタイル床にスノコを置いて、断熱タイプでなない
浴槽の場合は、前回ご紹介した1時間程度でコストが逆転するので、
使い方は、ご自宅の実態をご検討されると良いかと思います。
度々の修正で分かりにくかったかと思いますが、ご勘弁を。![]()
では、また。![]()