同じ誕生日の人
![]() 毎度のお付き合いをありがとうございます。
毎度のお付き合いをありがとうございます。
最近、
計算とは関係ない書き込みが多いので、そろそろ小出しに行きたいと思います。
さて、皆さんのお子様(小学校とか幼稚園など)でも身の回りでも良いのですが、
同じ誕生日の子(人)が偶然にしては、感覚的に多いような気がしませんか?
今回は、これについて計算してみようと思います。
まずは、簡単のため、同じ誕生月の人がどれほどの確率になるかを考えてみます。
計算方法ですが、まず2人の場合から考えます。
それぞれが違う誕生月の確率は、
簡単に、11/12×100%≒91.67%となりますが、
同じ誕生月の確率は、これの逆なので100%-91.67%=8.33%
となって、ほとんど一緒にならないですね。
感覚的にも、そんな感じかなぁと思います。
では、6人ならどうでしょう。
まず最初の2人が違う誕生月の確率は、 11/12
次の3人目は他の2人とも違う月なので、 10/12
次の4人目は他の3人とも違う月なので、 9/12
次の5人目は他の4人とも違う月なので、 8/12
最後の6人目は他の5人とも違う月なので、 7/12
となって、全ての確率を掛け算すると、22.3%となりますが、
同じ誕生月の確率は、これの逆なので100%-22.3%=77.7%
何となく、6人なら感覚的には半分の50%かなとも思いますが、
計算してみると、感覚よりも多いことが分かります。
じゃぁ、12人いたら100%になるのかって?
同じように計算すると、99.995%となって100%にはならないのです。
不思議ですねぇ。
では、同じ誕生日で計算してみましょう。
理屈は、誕生月のときと同じです。(閏年は考えません)
では、5人ならどうでしょう。
まず最初の2人が違う誕生日の確率は、 364/365
次の3人目は他の2人とも違う日なので、 363/365
次の4人目は他の3人とも違う日なので、 362/365
最後の5人目は他の4人とも違う日なので、361/365
となって、全ての確率を掛け算すると、97.3%となりますが、
同じ誕生日の確率は、これの逆なので100%-97.3%=2.7%
もう、同じ日になるのは奇跡に近いですね。
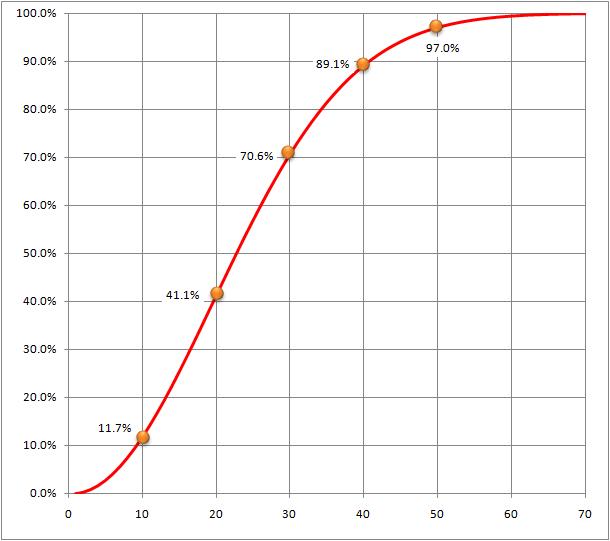
同じ計算を10人でやると、11.7%
20人なら、 41.1%
30人なら、 70.6%
40人なら、 89.1%
50人なら、 97.0%
となって、人数が増えると飛躍的に確率が増していきます。
今の小学校のクラス定員は、最大40人くらいなので、だいたいは90%
の確率で同じ誕生日の人がいるような計算です。
じゃぁ、100人いたら100%になるのかって?
同じように計算すると、99.99997%となって、やっぱり100%には
ならないのです。不思議ですねぇ。
では、今日はこのへんで![]()