月: 2010年8月

毎度のお付き合いをありがとうございます。
本日は、少しスケールアップしまして、富士山に挑戦したいと思います。
さすがに富士山ともなれば、すでに先人の方々によって色々な試みがされてます。
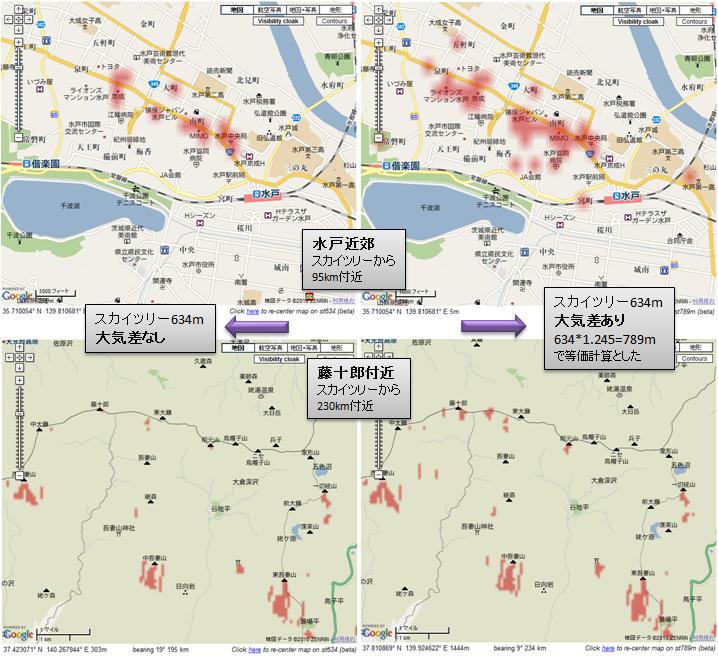
水戸の富士の回では、私が撮影した名峰富士の雄姿をご紹介しました。
スカイツリーと富士山では、大きさこそ違えど眺望計算としては同じ扱いになるので、
また、“Hey, what’s that?”の力を借りて計算してみました。
結果、北限の富士、最遠望の富士ともに更新の可能性が出てきました。
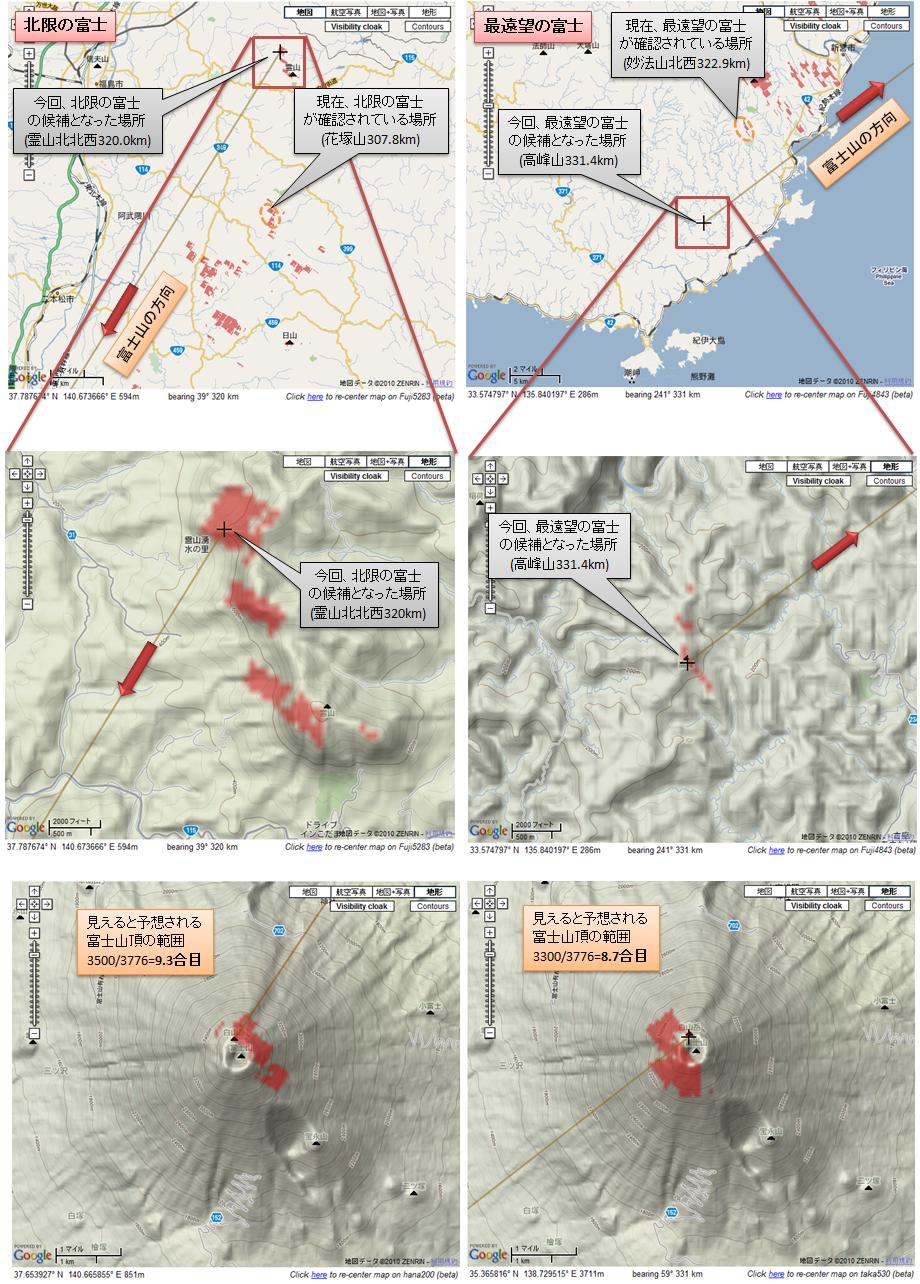
まず、北限の富士ですが。
私の予想では、現在確認されている福島県花塚山(307.8km)より更に１２ｋｍ北上した、
霊山の北北西(320.0km)が候補として挙がりました。
見え方としては、山頂から９．３合目が見える形になります。
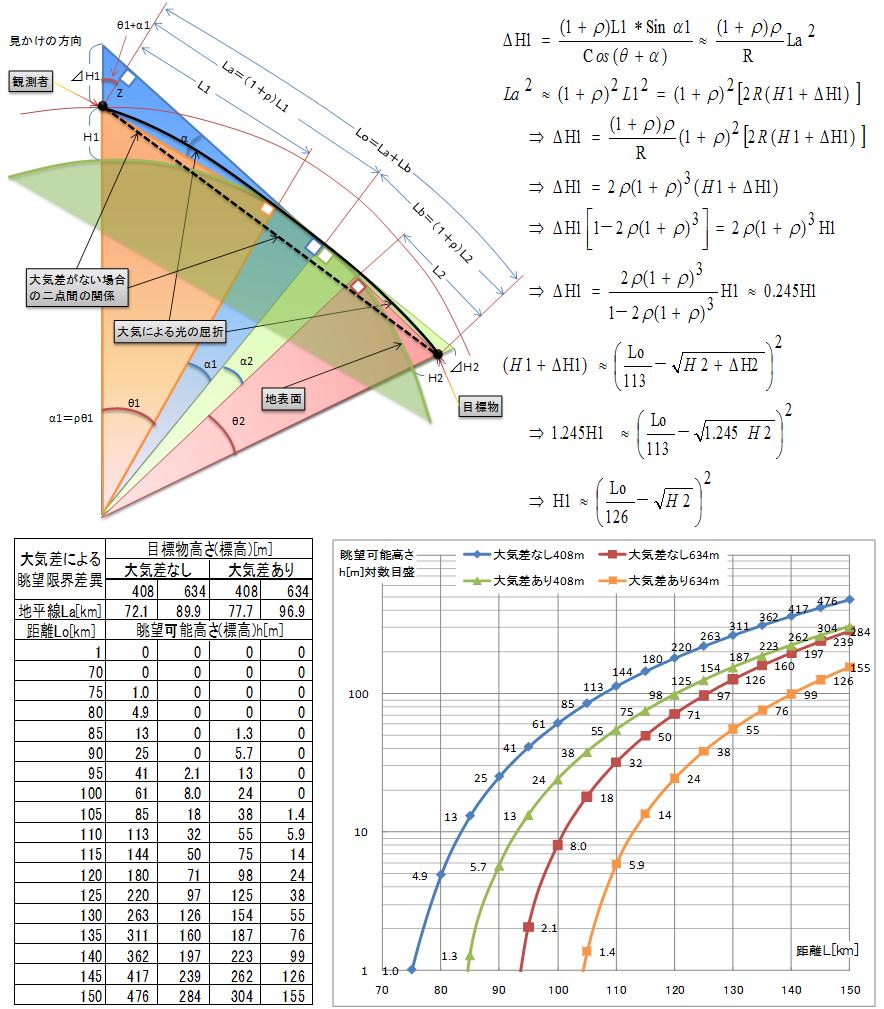
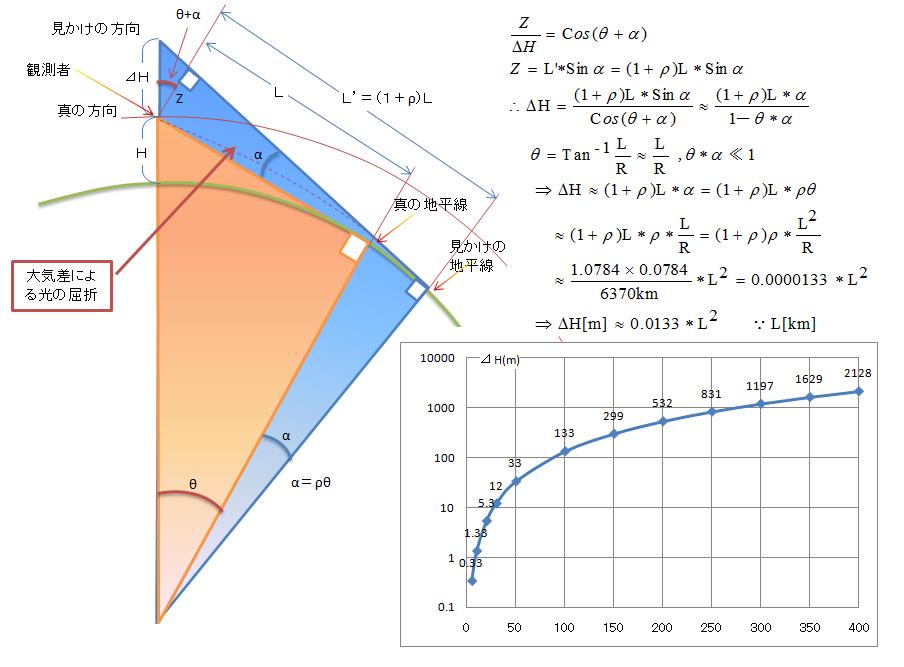
　計算諸元としては、大気差によるΔＨ増分として、富士山の標高3776*0.245=925m、
　霊山北北西の標高1200*0.245=294mは、それぞれからの水平線距離を按分(200:100)として、
　霊山北北西294*2=588mを富士山ΔＨ増分に加え、3776+925+588=5289mを大気差による等価的な
　富士山の標高として入力し、可視範囲を計算しました。
次に、最遠望の富士ですが。
私の予想では、現在確認されている和歌山県妙法山北西(322.9km)より更に８ｋｍ南下した、
高峰山(331.4km)が候補として挙がりました。
見え方としては、山頂から８．７合目が見える形になります。
　計算諸元としては、大気差によるΔＨ増分として、富士山の標高3776*0.245=925m、
　高峰山の標高290*0.245=71m、それぞれからの水平線距離を按分(200:100)として、
　高峰山71*2=142mを富士山ΔＨ増分に加え、3776+925+142=4843mを大気差による等価的な
　富士山の標高として入力し、可視範囲を計算しました。
腕に自信のある方(先人の方々へ)へのお願いになるかも知れませんが、
私の体力では、両地点ともに検証確認(撮影)は到底不可能です。
つきましては、この記事に少しでも可能性を感じて戴けた貴重な方には、是非とも検証確認のご検討
をいただければ幸いです。
その際、仮に今回の記事が発端となって、実際に行動され方が確認に成功された場合ですが、
新記録達成の権利(栄冠)の一切は、この場で放棄(お譲り★)致します。
(★私は、単に計算を趣味として、お遊びとしてやっているだけですので)
さて、今日も楽しんでいただけましたでしょうか。
今回は、少しスケールの大きい話題だったので、私も書きごたえありました。
では、今日はこのへんで。

毎度のお付き合いをありがとうございます。
さて、さきほどの計算のつづきになりますが、
大気差を考慮した場合の「スカイツリー　どこまで見えるマップ」の違いについて、
ご紹介したいと思います。
ここでは、大気差による地平線から見た高さ増分ΔＨ＝０．２４５Ｈの関係式から、
スカイツリーが１．２４５倍の高さ７８９ｍになったものと等価と考えました。
また、“Hey, what’s that?”により、違いを見てみましょう。
まず我が町、水戸市近郊での比較から。
大気差なしだと、水戸の高台となっている部分のほんの少しだけが可視範囲なのに対し、
大気差を考慮すると、中央の国道５０号周辺の大部分(泉町～南町～銀杏坂あたり)まで
可視範囲が広がっています。(非常にローカルな話で申し訳ありません)
一方、最遠方の福島県藤十郎付近ですが。
両条件の可視範囲に極端な差異は無く、何となく見える場所が広がっている程度でした。
このことから、
大気差による影響は、中距離程度(１００～１５０ｋｍ)で顕著となる傾向があるようです。
皆さんの町では、どうでしょうか？
では、今日はこのへんで。

お待ちいただいていた方には、遅くなり申し訳ありませんでした。
毎度のお付き合いをありがとうございます。
さて、今回は、大気差による影響をスカイツリーの計算に当てはめて見ました。
で、なかなかご披露できなかったのは、全体の計算確認に時間がかかってしまったこともありますが、
ペルセウス流星群に気を取られていたのが一番の原因とも。。。
(一時間粘って、やっと一筋だけ見えました)
結論としては、大気差による影響が思った以上に大きく、スカイツリーが
当初思っていたよりも、広い範囲で見えそうだということです。
なので、私の住む水戸でも　さほど高いところまで行かずに、十分にスカイツリーが見えるようです。
ますます、水戸からのスカイツリーが見たくなってきましたよ。
このつづきは、更に壮大な企画を考えておりますので、お楽しみに。
解説:大気差
　ご存知の方には今さらだと思いますが、
　大気の上層と地上との大気圧の差によって現れる現象で、大気圧の差＝屈折率の差であり、
　このことで光が連続的に曲線を描きながら屈折して進むことで、様々な現象を演じます。
　太陽や月などの場合、最大(0.572度)は、その視直径を上回る変化がありますので、
　例えは、日の出や日の入りの時、見えている太陽は　実は地平線の下にあるのです。
　私は、このスケールの大きさに驚いてしまいます。
では、また。

拙ブログを見に来ていただき、ありがとうございます。

今日は眠気に負けてしまいました。
申し訳ありませんが、つづきは　また明日にさせて戴きます。

大気差の発展計算について、構想がありますので、
結果まで辿り着かなくても、何かしらのカキコはできると思います。

ではでは、おやすみなさい。

毎度、計算ばかりやってますが、お付き合いください。
今回は大気差(大気による屈折の影響)について考察しました。
さて、高さＨ(m)から地平線までの距離は、Ｌ(km)＝３．５７√Ｈでした。
ところが、
実際は地平線と観測者の間で大気の影響(屈折)を受け、若干長くなるようです。
これをベッセル定数ρといって、標準大気でρ＝７．８４％としています。
今回は、この大気差の影響を、観測点Ｈ(m)の見かけの高さ増分ΔＨ(m)で
表現したいと思います。
結果は、下記のごとく、距離の自乗に比例する式が出ました。
具体的には、５０ｋｍ見通せる高さ(逆算すると１９６ｍ)から見た地平線は、
大気による光の屈折効果で、実際はその＋３３ｍの２２９ｍから見た地平線と
同じ方向で、距離も５０ｋｍの７．８４％遠い５３．９ｋｍまで見えるという計算です。
消化不良ですが、もうじきペルセウス流星群が見られそうなので、今日はこのへんで
終わりにします。
このつづきは、また明日～。。。